Je me lance un défis, vous présenter les résultats du module Yolland Bresson que j’ai réalisé il y a 3 ans. Je n’expliquerais pas ici les raisons du retard de publication mais ce que vous comprendrez aisément, c’est qu’il est difficile, en mars 2020, de se replonger dans ça
alors que le plus ancien fichier date de novembre 2016 et le plus récent de mars 2017, juste avant que je ne m’envole pour la dernière fois vers l’Iran.
Les données avaient été récupéré à l’aide des liens indiqués sur la page du module sauf celle concernant l’historique des prix des appartements que j’avais emprunté à ce pdf qui venait du site https://basebien.com , http://paris-notaires-services.fr/professionnels/base-bien/ [mais je ne sais pas si il est encore possible aujourd’hui d’obtenir ce genre de pdf gratuitement] et aussi le site www.notaires.fr/.
Le module se déroule en trois parties:
1 – Comparer l’évolution de certaines valeurs entre elles sur de longues périodes
2 – Étudier l’évolution du prix du m2 relatif à certaines unités de valeurs en deux lieux sur de longues périodes
3 – Comptabilité (en partie double) au sein d’une monnaie libre
1 – Évolution de certaines valeurs entre elles sur de longues périodes
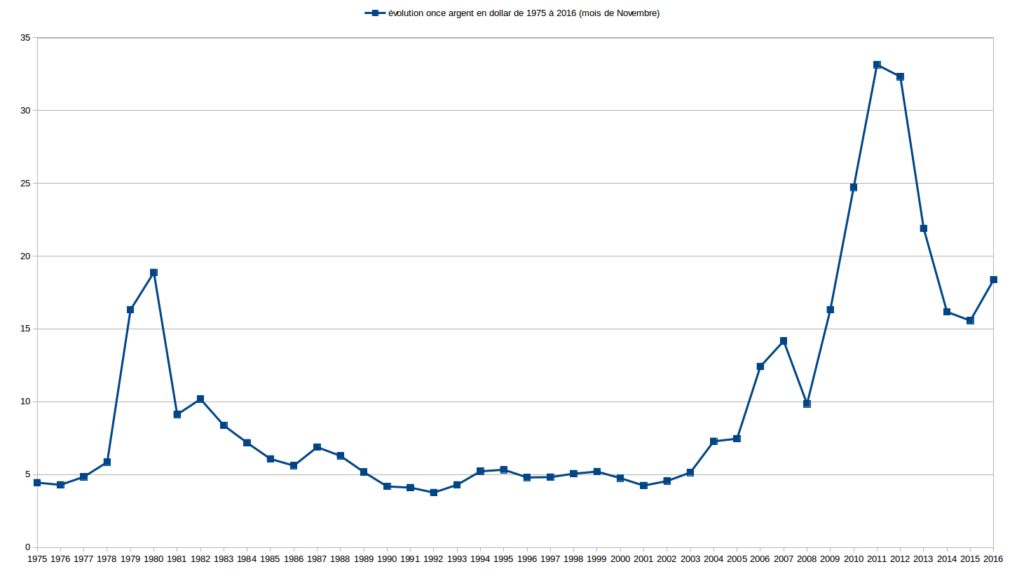
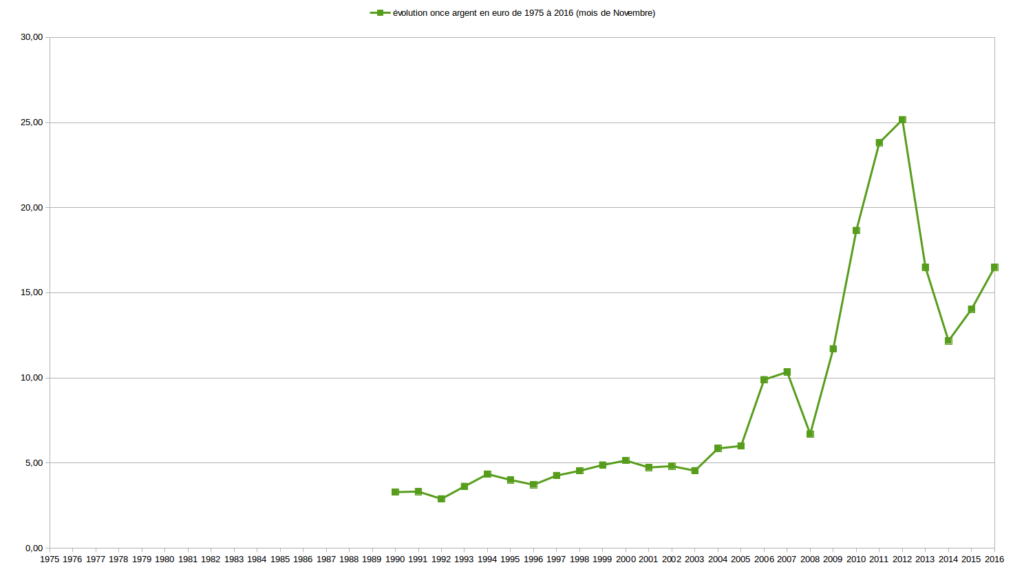
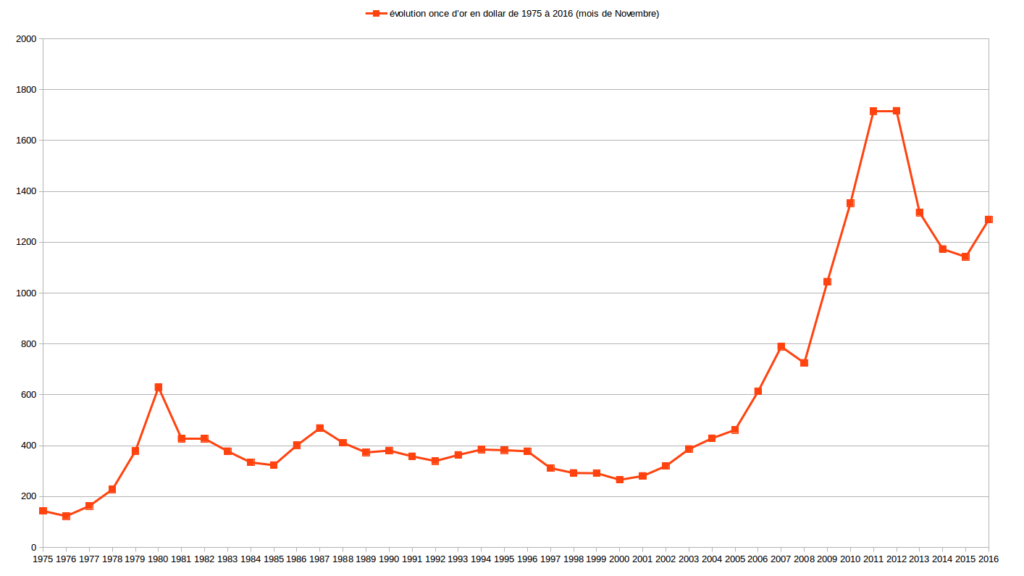
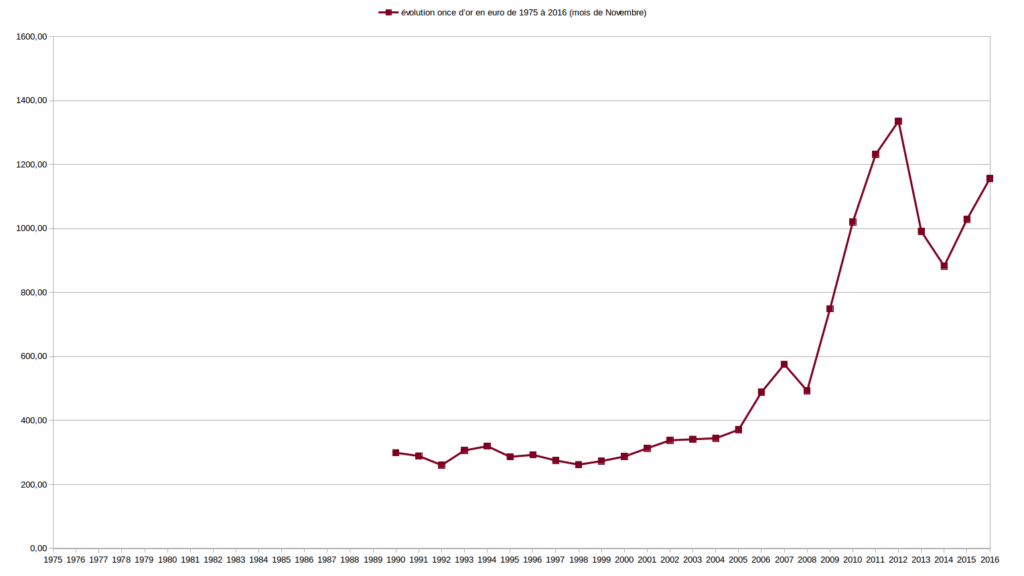
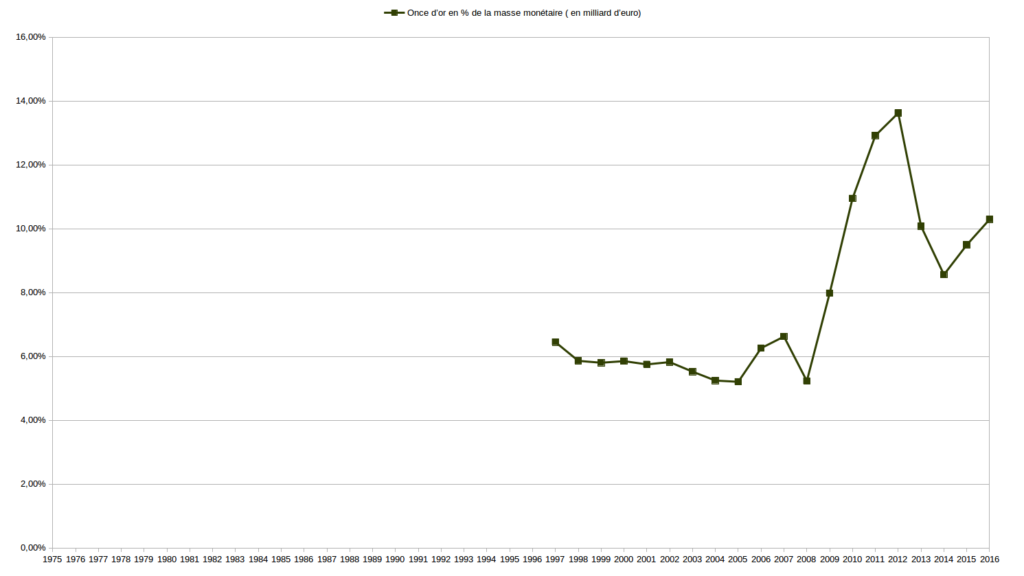
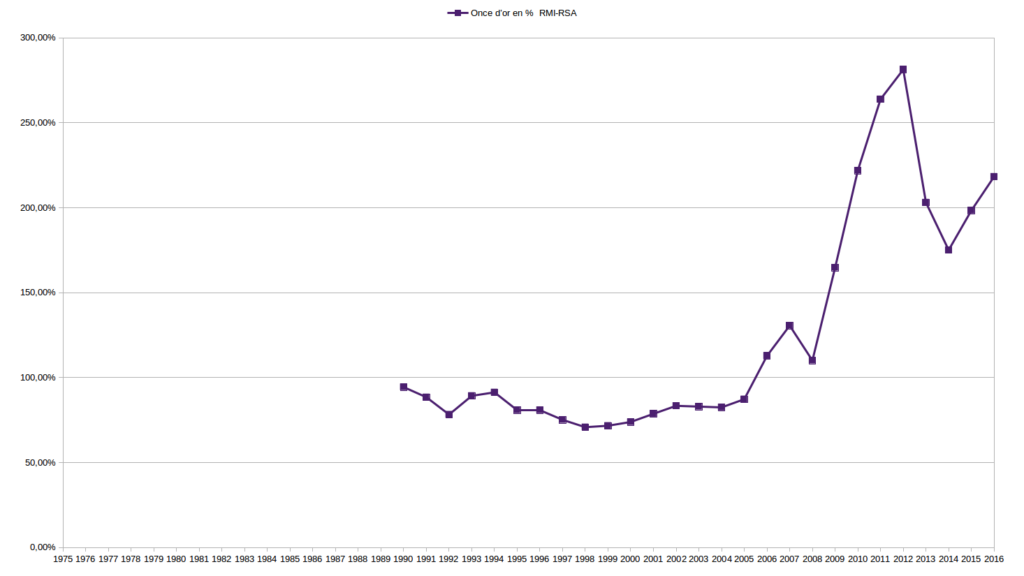
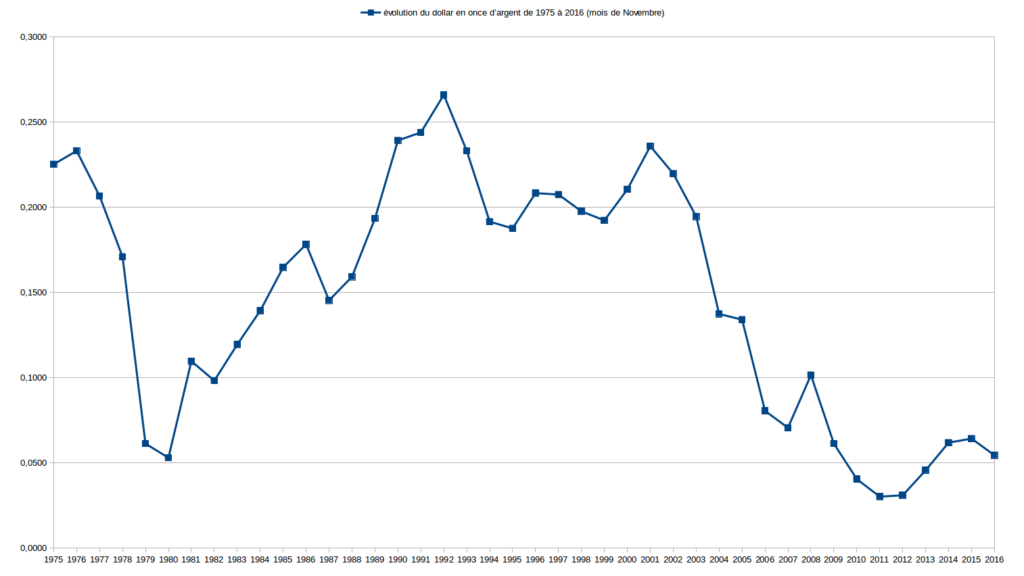
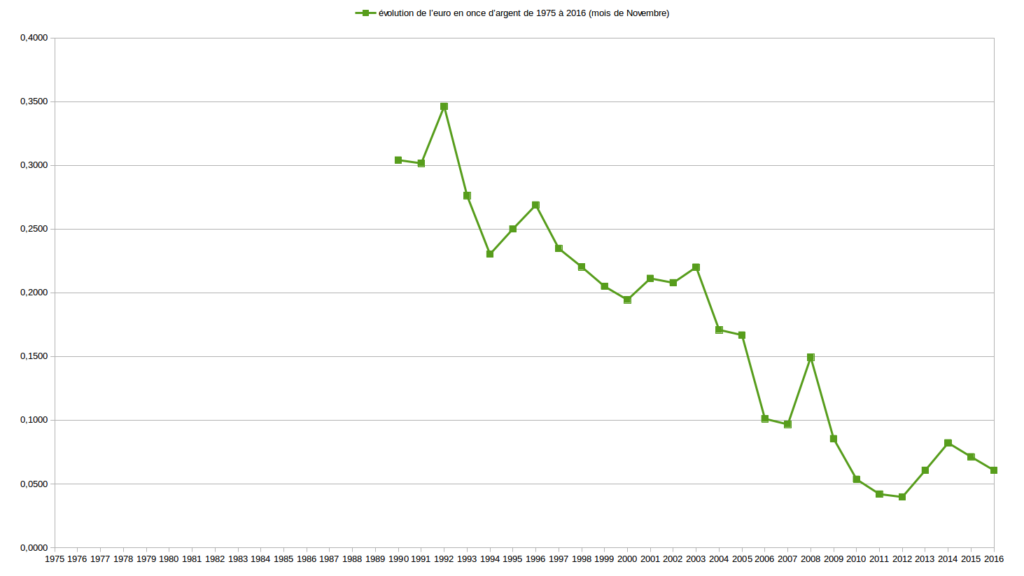
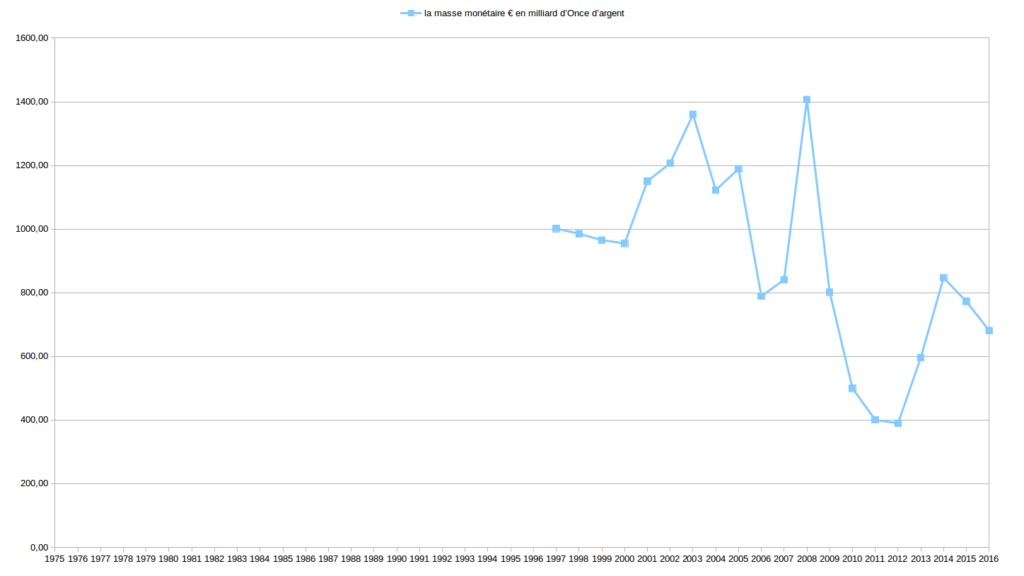
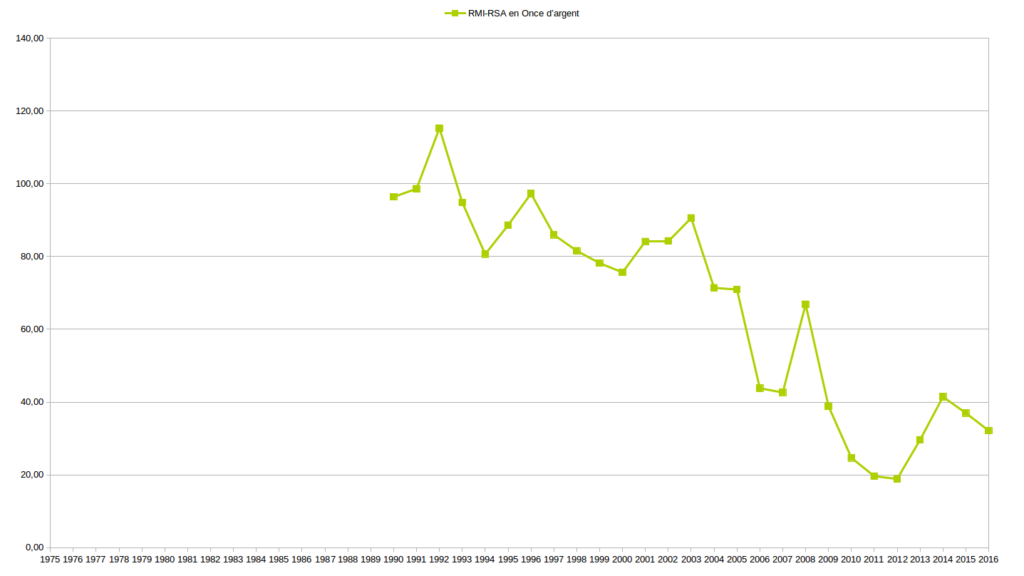
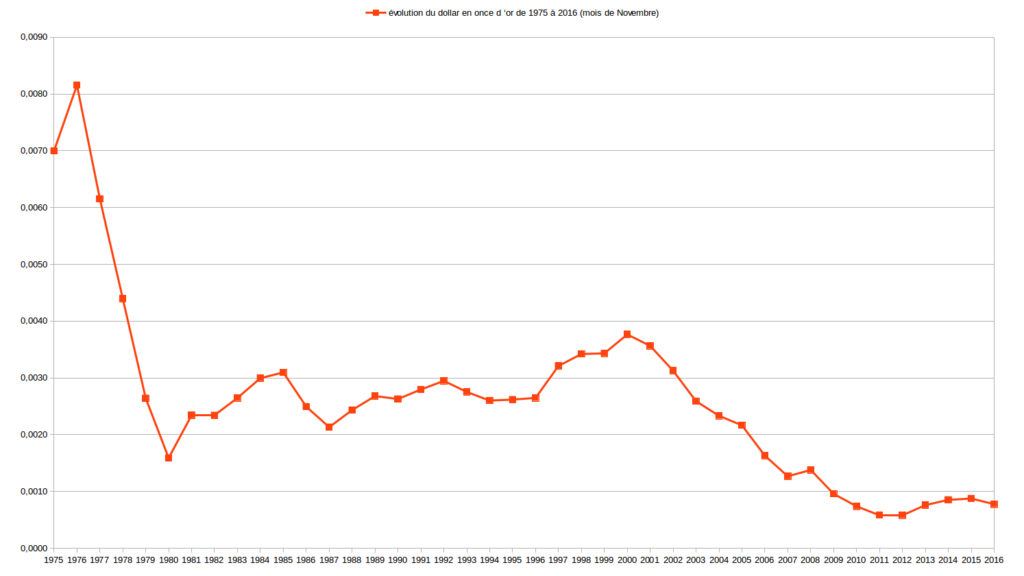
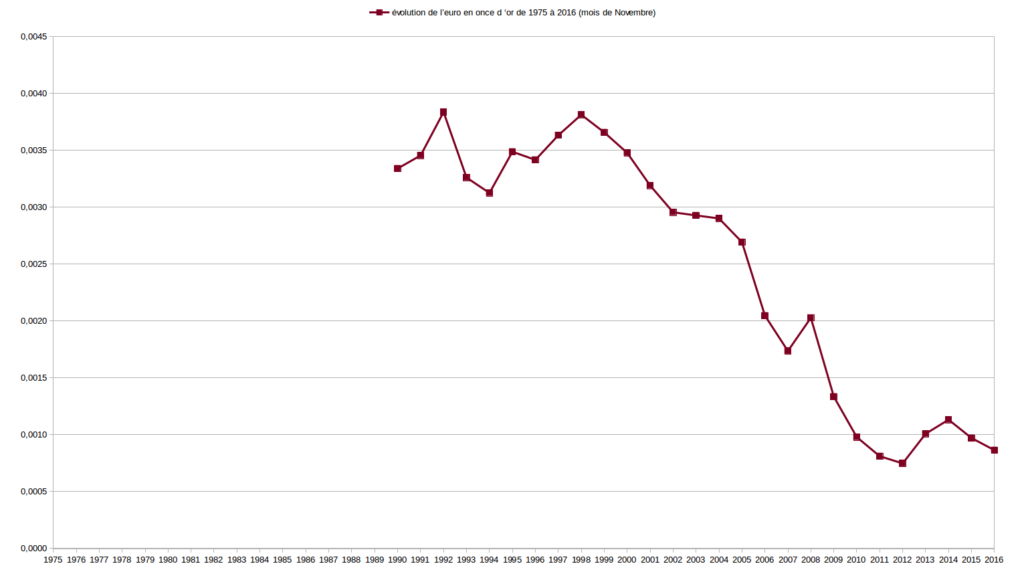
Sur de longues périodes, allant de 1973 (parfois plus tard, selon les données disponibles) à 2016, j’ai comparé l’évolution des valeurs Or, Argent, $ et € relativement entre elles d’abord puis les ai étudié en fonction de la masse monétaire € et du RMI/RSA. Je vous expose un certains nombres de ces graphiques ci-dessous.
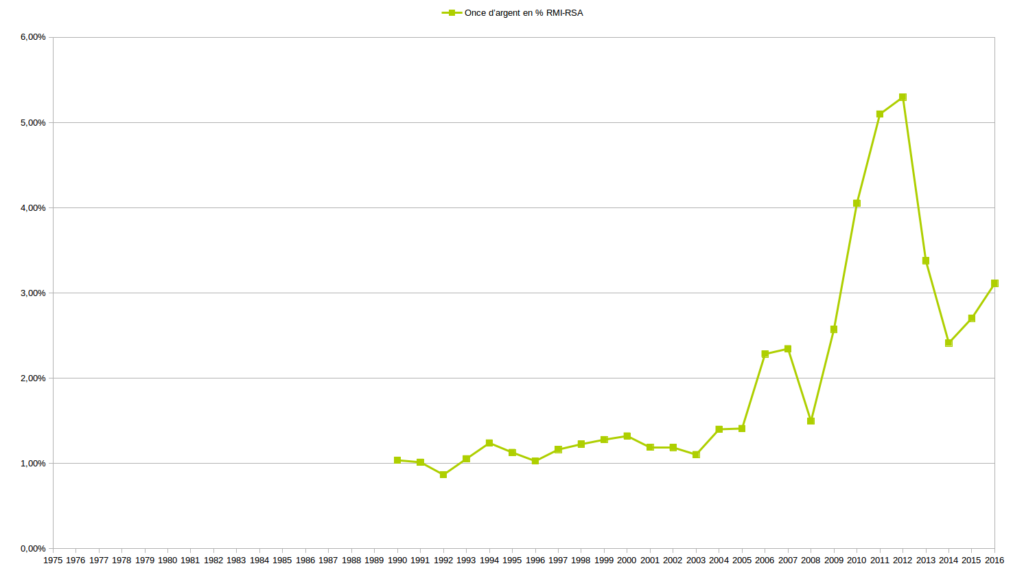
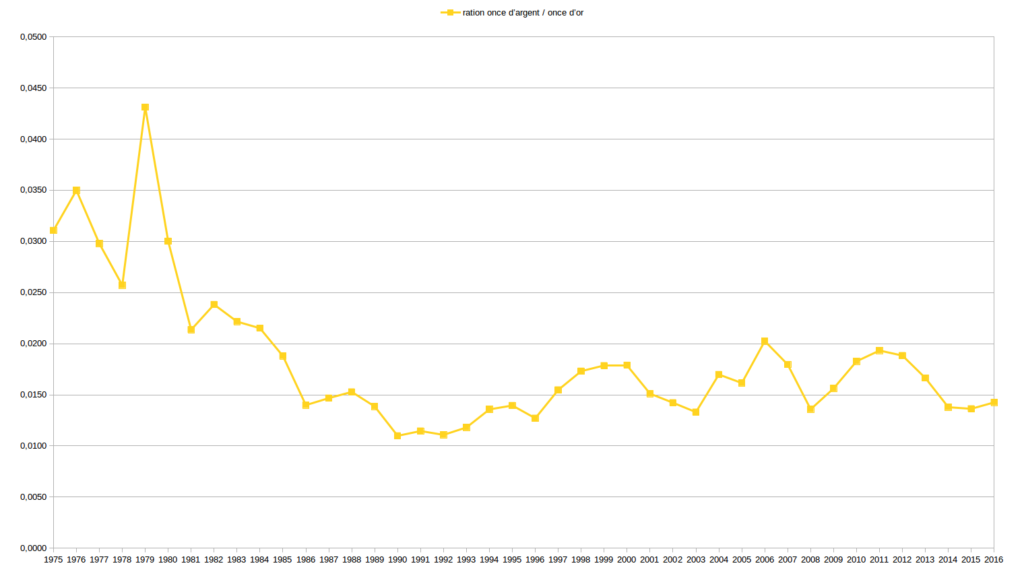
Les deux graphiques suivant sont ceux de l’évolution des valeurs Or et Argent exprimées l’une par rapport à l’autre.
Je serais curieux de me faire expliquer ces graphiques par ceux qui martèlent qu’il existe des valeurs de référence comme l’Or ou l’Argent sur lesquels les monnaies devraient absolument s’adosser. Pour ma part, ces graphiques ne me donnent pas particulièrement confiance au couple Or/Argent.
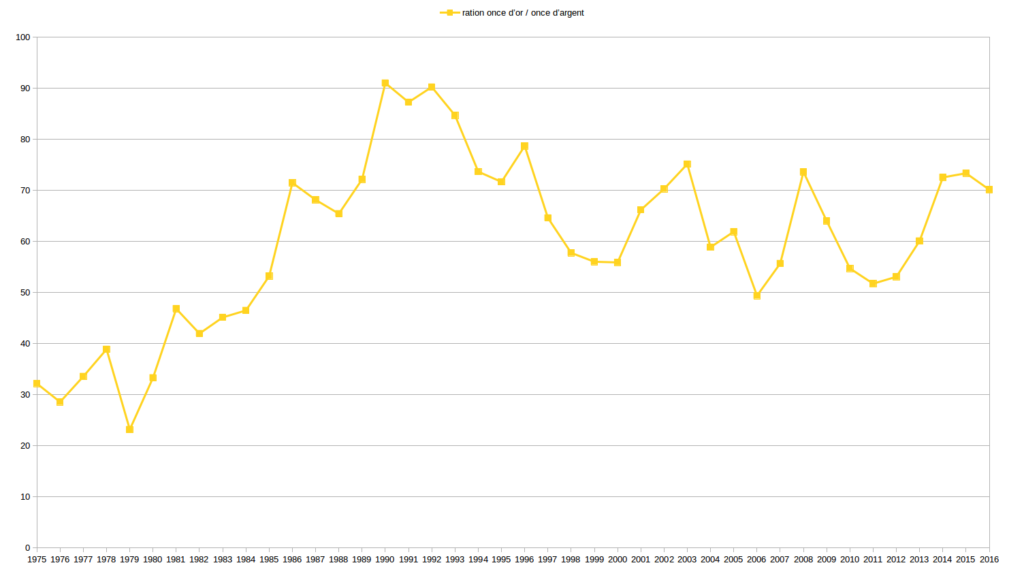
Ci-dessous sont publiés les graphiques inverses des premiers.
2 – Évolution du prix du m2 relatif à certaines unités de valeurs à Paris et en province sur de longues périodes
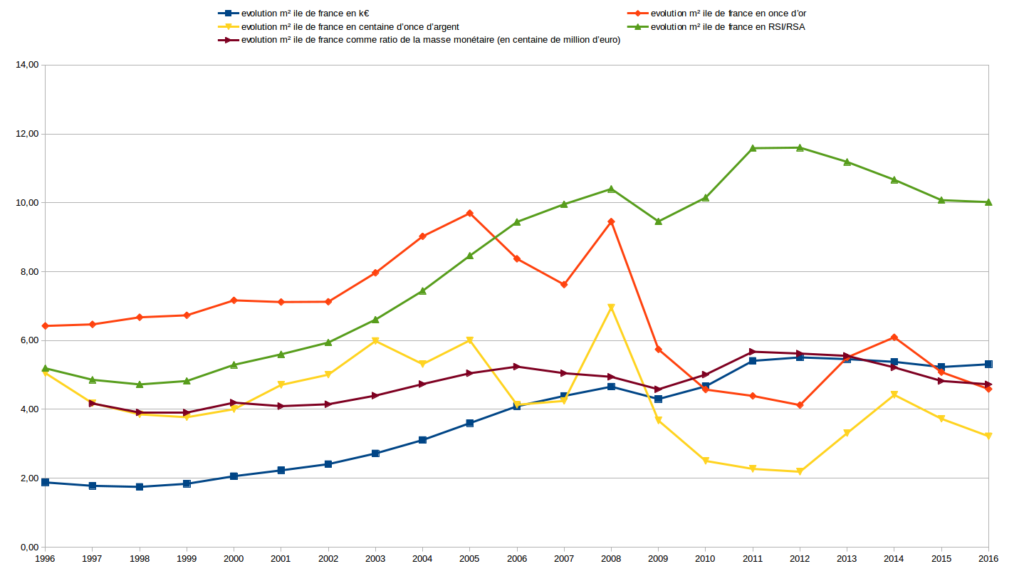
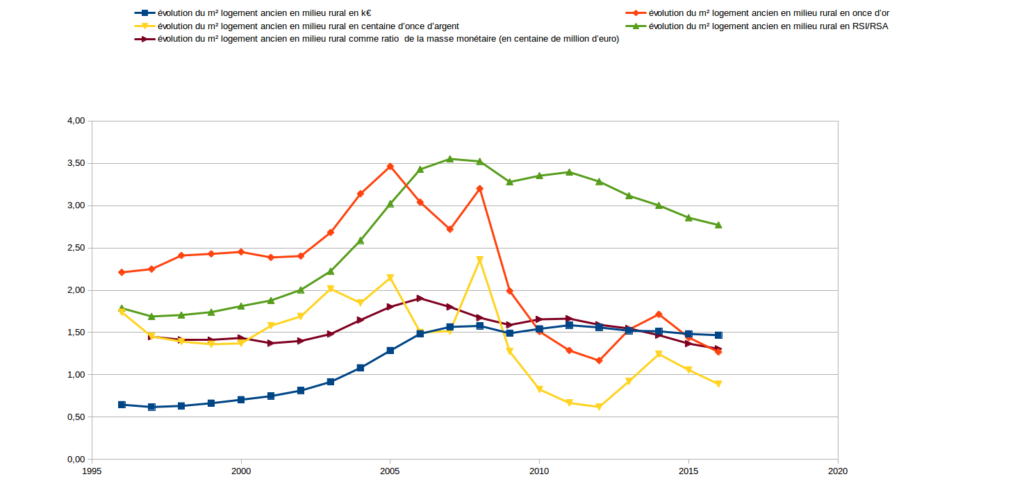
Dans cette partie, j’ai étudié l’évolution du prix du m2 à Paris dans le temps ainsi que (attention jargon de l’INSEE) celui du “prix des logements anciens – Province : agglomérations de moins de 10 000 habitants et zones rurales – Appartements – Base 100”. J’ai exprimé l’évolution de ce prix relativement aux valeurs étudiés ci avant.
Encore une fois, on remarque que les courbes de valeurs exprimées en Or et en Argent sont décorrélées. Au début, la courbe rouge monte quand la jaune descend. On le voit nettement aussi entre 2003 et 2005.
Si l’échelle des prix est bien différente entre Paris et le logement ancien en province comme je m’y attendais, je suis surpris de constater que les évolutions du prix à Paris et en province suivent sensiblement les même courbes alors que je pensais ces marchés beaucoup plus indépendants. Peut être est-ce dû au fait que le prix du logement ancien en province soit un prix moyen sur l’ensemble du territoire.
Est-ce que l’étude d’un marché immobilier singulier de province comme celui de la Creuse ou celui d’un DOM/TOM suivrait lui aussi le marché parisien? À vérifier.
En revanche, on voit bien sur le graphique du dessous qu’une affirmation péremptoire disant que le marché du logement ancien s’effondre en 2010 n’est vraie qu’à condition de mentionner “relativement à l’argent”. C’est faux relativement au RSA.
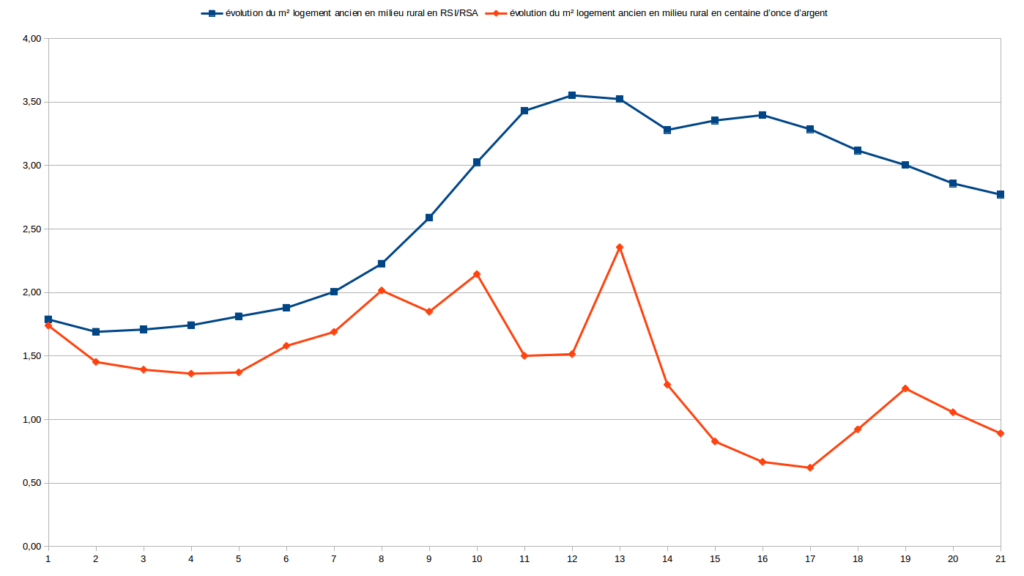
On s’en aperçoit encore mieux je trouve dans ce petit gif animé que j’avais réalisé.
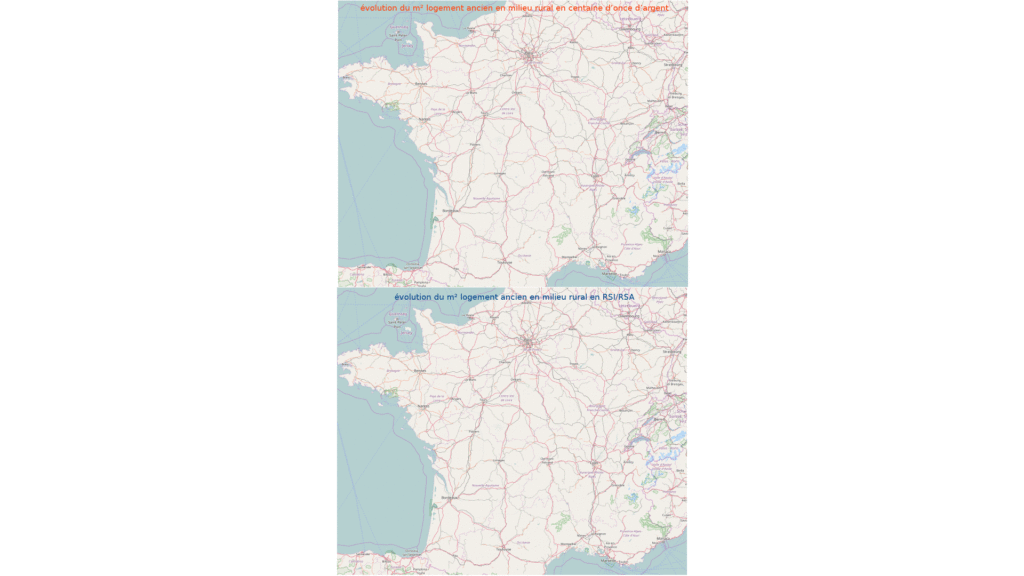
3 – Comptabilité (en partie double) au sein d’une monnaie libre
Dans cette partie, j’ai commencé par simuler une économie monnaie libre sans échange entre 30 individus qui se succèdent sur 160 ans.
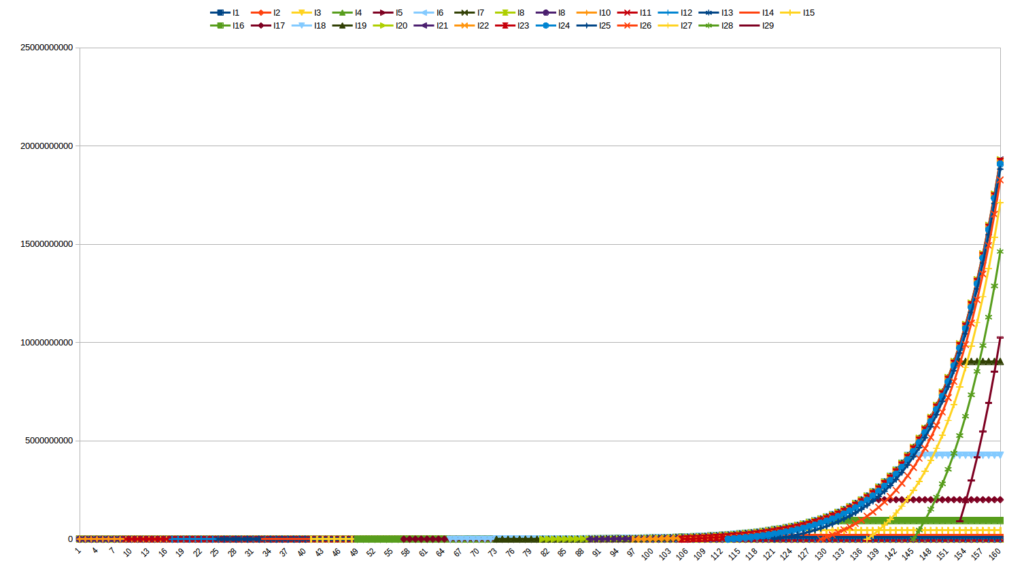
Ce graphique est intéressant pour se rendre compte que les premiers entrants ne sont pas les plus avantagés (voir les couches du bas, celles de la monnaie “capitalisée” pendant toute la vie des premiers individus et disparue avec leurs morts) et que le dernier arrivant, I29, qui pourtant n’existe que pendant les 7 dernières années de la simulation tend très rapidement à rejoindre “l’économie” en place.
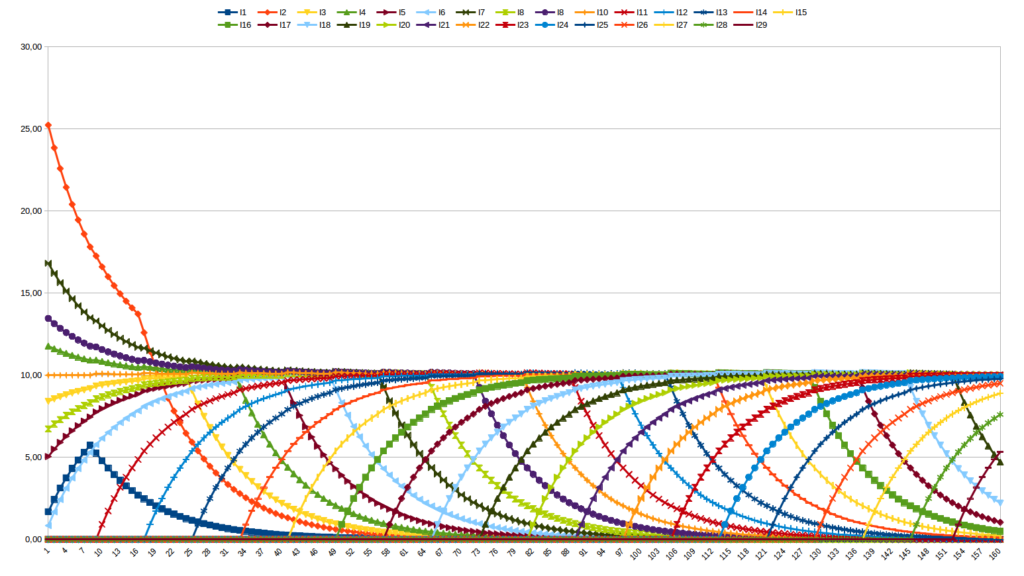
Ce graphique est celui de la quantité de monnaie qu’a chaque individu divisé par le DU du moment. On voit bien la tendance vers la moyenne de 10 DU (c’est une simulation avec à chaque instant t seulement 10 individus vivant).
Si on décide de simuler trois échanges monétaires à 3 instants t entre les individus I4 et I7 ainsi qu’un quatrième échange entre I15 et I17, ce même graphique devient le suivant et souligne encore plus fortement cette tendance vers la moyenne. Je ne publie pas le graphique en quantitatif car il ne montre aucune perturbation, les échanges étant trop petits par rapport à la masse monétaire finale [qui allonge l’échelle].
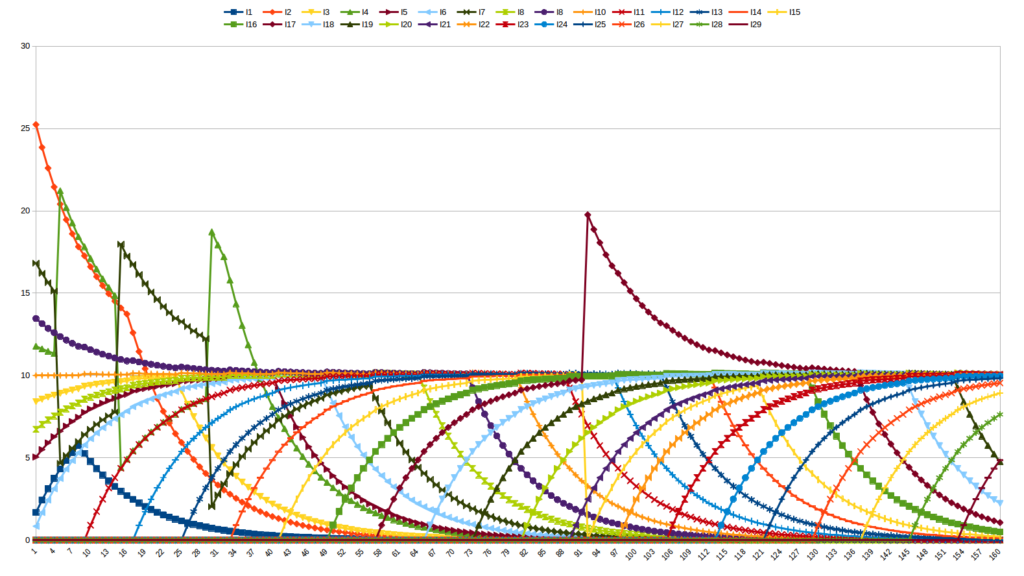
Les échanges entre I4 et I7 sont tels que :
– en l’an 5, I4 vend des biens ou services à I7 pour un montant de 8703
– en l’an 15, c’est I7 qui vend des biens ou services à I4 pour un montant de 22369
– en l’an 30, I4 vend de nouveau des biens et services à I7 pour un montant de 91748
La comptabilité en partie double de ces 3 années pour ces trois individus, du point de vu de l’individu Ix (Iy ayant une autre appréciation des valeurs et parlerait donc en Ğ(y)) pourrait être écrite comme suit :
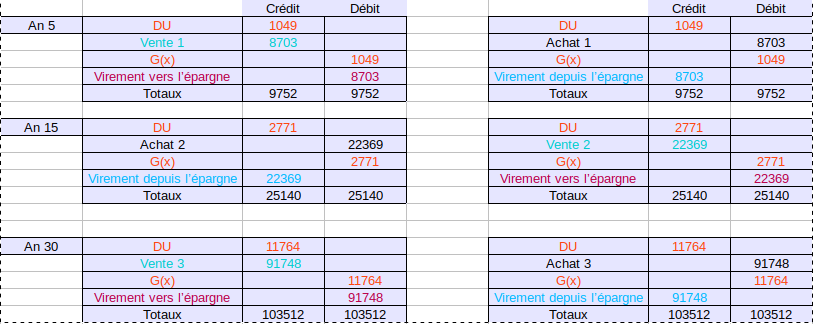
Qu’est-ce que Ğ(x) vous demandez-vous? Et bien Ğ(x) est la valeur qu’un individu n’est pas en capacité de nommer. Ix n’est même pas en capacité de dire si Ğ(x) est une valeur ou une non valeur.
Ğ(x) permet de pointer du doigt l’existence de production de valeurs inconnaissables que le DU dans une économie à monnaie libre finance. En effet, nous ne sommes pas toujours conscients des valeurs que nous produisons et ce n’est que plus tard qu’elles peuvent être révélées comme telle, parfois même, après notre mort. Dans ce dernier cas, dans une économie sans DU, le producteur de valeur pourrait ne jamais être rémunéré pour sa contribution.
Ğ(x) dépend évidement de l’observateur. Mon exemple précédent vu par Iy (qui connaît très bien I4 et perçoit une capacité créatrice avant-gardiste chez I4) pourrait être :

Y2 et Y3 étant d’après l’individu Iy des versions améliorées de Y1. Notez que Y1, Y2 et Y3 ne sont pas observées par l’individu Ix comme des valeurs, il n’a pas conscience/connaissance des innovations que Iy perçoit lui.
Ainsi, G(y) dans la comptabilité en partie double de I4 est toujours plus faible que G(x).
Conclusion
Me replonger dans ce module afin de le publier et de vous rendre mon travail accessible, m’a permis de reprendre pleinement conscience de la relativité des valeurs. Un prix qui monte ou baisse d’accord, mais mesuré avec quelle valeur de référence (or, argent, RSA, plume d”oie)? et où? à Paris? dans le Finistère? et à quelle période?
En replongeant dans les simulations d’économie à monnaie libre en quantitatif et relatif j’ai pût mettre en avant de nouveau la beauté de l’équité temporel (entre génération) et de la tendance à la moyenne.
Enfin, lors de ce module, on doit se poser la question des “valeurs” imperceptibles, celles qui sont produites sans être mesurées, ni même parfois mesurables par l’observateur. L’observateur, singulier ou pluriel (une société entière) peut ne pas être en mesure de quantifier/qualifier la valeur d’une découverte (parfois même ne pas mettre tout de suite le mot découverte sur ce qui en est une) ou d’une création.
Mon fichier de calcul est téléchargeable ici.